2024. 1. 14. 19:35ㆍPLAYS
[1막 4장]
(배경 : 현대의 시들리 파크)
한나와 발렌틴은 같은 공간에 있다. 한나는 토마시나가 적었던 카오스이론에 관한 기록을 발견한다. 이 이론은 발렌틴의 연구방식과 동일하며, 20세기가 되어서야 상용화된 이론이라는 게 드러난다. (마치 고대 동굴벽화에서 e=mc2공식을 발견한 것처럼 시대적으로 불가능한 상황) 바이런은 시들리 파크에 머무르고 있었다는 것이 사냥북을 통해 밝혀진다. 다른 사람들은 버나드의 논리에 헛점을 지적했음에도, 버나드는 오만하게 반응하며 바이런이 채터를 결투에서 죽인 것이라 확신한다.
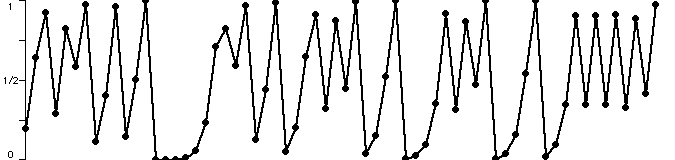
발렌틴의 반복 알고리즘(iterated algorithm)
19세기 시들리파크 뇌조의 증감율로 인구수를 예측하고자 하는 발렌틴의 방식은 20세기(작중 언급되길 20년 이내)에서야 사용됨. 그 이유는 어렵지는 않으나 엄청나게 반복해야 되는 계산식이라 컴퓨터 기술이 필요해서. 그러나 발렌틴처럼 과거의 데이터로 미래를 예측하는 방정식을 만들기 위해서는 노이즈(예측하지 못할 외부 요건)도 고려해야 됐었음.
한 해 새들의 수를 세는데 갑자기 여우 수가 늘었다던가, 기후변화라던가. 결과적으론 방정식을 통해 오히려 더 무작위적인 결과를 발견할 수 있음. . 나비효과처럼 초기에 가져온 약간의 변화가 시간이 지나면서 더 큰 결과를 가져올 수 있고.
토마시나가 적은 이론은 작중 언급된 것처럼 아이슈타인의 상대성이론같이 거창한 계산식이 아니었음. x값을 통해 y값을 구하고, 방금 구한 y값을 다시 x값으로 계속 계산하면 되니까. 그러나 20세기에선 컴퓨터로는 몇 분 만에 연산이 가능하나 손으로 작업하면 수십년이 걸리는 반복계산이 필요하니 그 누구도 볼 수 없는 거였음. 이를 18세기에 밝혀내려면 충분한 시간과 많은 종이가 필요하고, 약간 미쳐있으며 계산을 해야 할 이유가 있어야 했음. 마치 마지막에 한나가 집었던 콘힐매거진에 기록된 시들리파크의 은둔자처럼.
더 자세한 수학적 설명은 https://math.bu.edu/DYSYS/arcadia/sect5.html 여기에서.
카오스 이론 (혼돈이론 chaos theory)
우주는 무작위처럼 보이지만 비선형 방정식을 통해 날씨, 동물 개체 수 증가 등 예측할 수 없는 형상을 반복 패턴을 통해 확인할 수 있다는 이론. 1970년대 처음으로 발견되었다(작중 20년 전)
그래서 발렌틴이 뇌조를 통해서 개체 수를 구하려 한다던가, 몇 천년 전 이집트 날씨와 지금 영국 날씨 패턴을 같을 것이다 예시로 들었던 것도 그 이유.
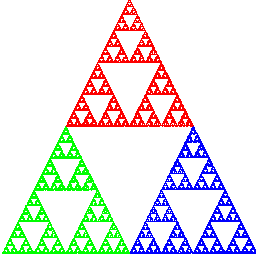
토마시나의 이론을 가장 잘 보여줄 수 있는 예시는 '시에르핀스키 삼각형 Sierpiński triangle'이라는 프렉탈 도형일 듯. 발렌틴이 말한 것처럼 삼각형 내의 점은 어디에 찍힐지 예상할 수 없으나, 수많은 점들이 찍히다보면 균일한 그 모습이 보이기 시작하는 것처럼.
그래서 세상은 3일 후 가든파티에 비가 올 확률처럼 예측할 수 없는 일과 은하계 모서리나 원자 내부처럼 이미 결정된 일이 함께 존재하는 것이라고.
언젠가 사과 이파리에 대한 계산식을 만들 것이다 라고 했던 토마시나의 발언(1막 3장)은 발렌틴이 말했던 것처럼 반복적인 알고리즘을 만들 수 있음. 고사리 양치식물(Barnsley fern)처럼 잎 모양의 점들을 확대하면 또다른 잎이 보이는 프렉탈 도형처럼.
호레이스 월풀 Horace Walpole
1막 1장에 언급되었던 그 고딕소설 작가

갈릴레오 Galileo(1564-1642)
이탈리아의 천문학자이자 과학자. 망원경을 통해 코페르니쿠스의 지동설을 입증했다.
'PLAYS' 카테고리의 다른 글
| 아우터 와일즈(outer wilds) 속 과학(2) : 엔딩까지의 양자역학과 천체물리학 (3) | 2024.01.28 |
|---|---|
| 아우터와일즈(outer wilds) 속 과학(1) : 인디게임 개발 제작 과정과 스토리 모티브 요약 (2) | 2024.01.23 |
| 연극 아카디아(Arcadia 아르카디아)의 줄거리, 용어 해설 소개 (3 - 1막 3장) (1) | 2024.01.06 |
| 과학연극 아카디아(Arcadia 아르카디아)의 배경, 작품 속 용어 해설 정리 (2 - 1막 2장) (1) | 2024.01.03 |
| 과학연극 아카디아(Arcadia 아르카디아)의 배경, 작품 속 용어 해설 정리 (1 - 1막 1장) (4) | 2024.01.02 |